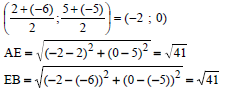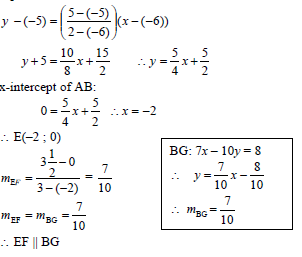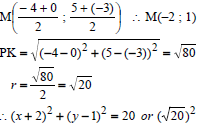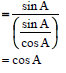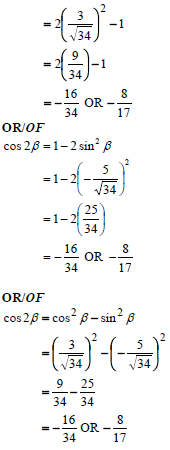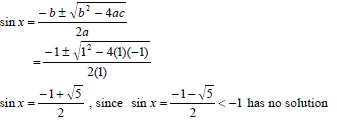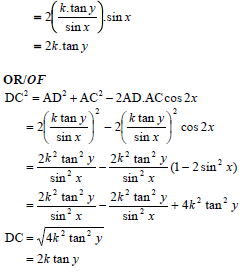GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2017

Friday, 23 July 2021 06:59

GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2017

More in this category: « ACCOUNTING GRADE 12 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2017 GRADE 12 MATHEMATICS PAPER 2 QUESTIONS - NSC PAST PAPERS AND MEMOS NOVEMBER 2017 »

Share via Whatsapp Join our WhatsApp Group Join our Telegram Group

MATHEMATICS PAPER 2
GRADE 12
NOVEMBER 2017
MEMORANDUM
NATIONAL SENIOR CERTIFICATE

NOTE:

If a candidate answers a question TWICE, only mark the FIRST attempt.
If a candidate has crossed out an attempt of a question and not redone the question, mark the crossed out version.
Consistent accuracy applies in ALL aspects of the marking guidelines. Stop marking at the second calculation error.
Assuming answers/values in order to solve a problem is NOT acceptable.

GEOMETRY
S	A mark for a correct statement (A statement mark is independent of a reason.)
R	A mark for a correct reason (A reason mark may only be awarded if the statement is correct.)
S/R	Award a mark if the statement AND reason are both correct.

QUESTION 1

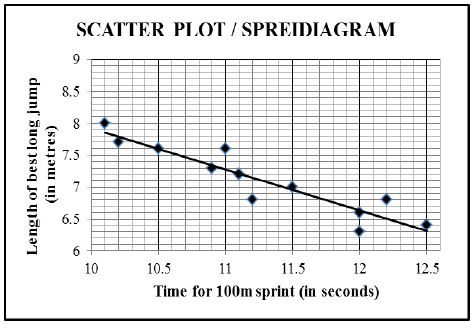
Time for 100 m sprint (in seconds)	10,1	10,2	10,5	10,9	11	11,1	11,2	11,5	12	12	12,2	12,5
Distance of best long jump (in metres)	8	7,7	7,6	7,3	7,6	7,2	6,8	7	6,6	6,3	6,8	6,4

1.1	a = 14,343… = 14,34 b = –0,642… = – 0,64	✓✓ value of a ✓ value of b (3)
1.2	Y = 14,42 - 0,64(11,7) OR y = 6,83 (calculator)	✓ substitution correctly ✓ answer (2) ✓✓answer (2)
1.3	The gradient increases The point (12,3 ; 7,6) lies some distance above the current data.	✓ increases ✓ reasoning in words (2)

[7]

QUESTION 2

12	13	13	14	14	16	17	18	18	18	19	20
21	21	22	22	23	24	25	27	29	30	36

2.1.1	x = 472 23 x = 20,52 seconds	✓ 472 23 ✓ answer (2)
2.1.2	Q₁ = 16 Q₃ = 24 IQR = Q₃ – Q₁ = 24 – 16 = 8	✓ Q₁ ✓ Q₃ ✓ answer (3)
2.2	20,52 + 5,94 = 26,46 ∴ > 26,46 ∴ 4 girls	✓ 26,46 ✓ answer (2)
2.3		✓ whiskers ending at 12 & 36 ✓ Q₁ = 16 & Q₃ = 24 (box) ✓ Q₂ = 20 (3)
2.4.1	Girls	✓ answer (1)
2.4.2	Five-number summary of boys: (15 ; 21 ; 23,5 ; 26 ; 38) None of the boys 5 girls completed in less than 15 seconds which was the minimum time taken by the boys.	✓ answer ✓ reason/(2)

[13]

QUESTION 3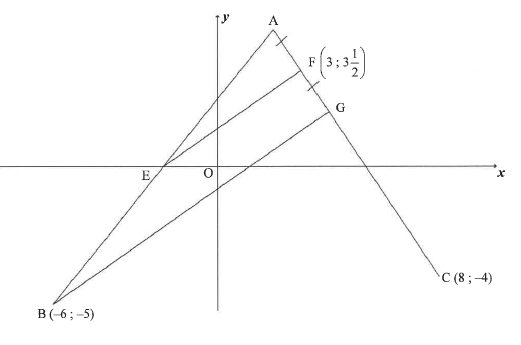

3.1.1	mFC = y₂ - y₁ x₂ - x_1 = 3½-(-4) 3-8 = - 3 2 y = mx + c y - y1 = m(x-x1) y = - 3 x + c 2 -4=- 3 (8) + c OR (y-(-4))=- 3 (x + 8) 2 2 y = - 3 x+8 y+4 = - 3 x + 12 2 2 y = - 3 x + 8 y=- 3 x + 8 2 2 OR	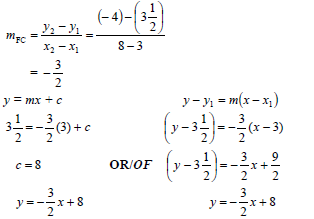✓ substitution of (8 ; –4) & (3;3½) ✓ gradient ✓ substitution of m and (8 ; –4) ✓ equation of AC (4) ✓ substitution of (8 ; –4) & (3;3½) ✓ gradient ✓ substitution of m and (3;3½) ✓ equation of AC (4)
3.1.2	AC: 3x + 2y = 16 and BG: 7x – 10y = 8 15x + 10y = 80 7x – 10y = 8 22x = 88 x=4 3(4) + 2y = 16 y=2 ∴G(4 ; 2) OR BG: 7x – 10y = ∴ 7 x- 8 10 10 ∴ 7 x- 8 =- 3 x + 8 [CA from 3.1.1] 10 10 2 11x = 44 5 5 x = 4 3(4) + 2y = 16 y = 2 ∴G(4 ; 2)	✓ method:solving simultaneously ✓ x coordinate (x > 0) ✓ y coordinate (3) ✓ method: equating ✓ x coordinate (x > 0) ✓ y coordinate (3)
3.2	x₄ + 4 =3 and y_A + 2 = 3½ 2 2 ∴ A(2 ; 5) OR by translation: x_A = 3-(4-3) = 2 y_A = 3½+(3½-2)=5 ∴ A(2 ; 5)	✓ equation ito x ✓ equation ito y (2) ✓ equation ito x ✓ equation ito y (2)
3.3	The coordinates of the midpt of AB: But the y-coordinate of E is 0 ∴ E(–2 ; 0) is the midpoint of AB ∴ EF \|\| BG [midpoint theorem OR line divides 2 sides of Δ in prop/lyn] OR The coordinates of the midpt of AB is: ∴ In ΔABG: AE = EB and AF = FG ∴ EF \|\| BG [midpoint theorem] OR Equation of AB:	✓ subst A & B into midpt formula ✓ y coordinate = 0 ✓ E = midpt ✓ Reason (4) ✓ subst A & B into midpt formula ✓ lengths of AE & EB ✓ AE = EB or E = midpt ✓ Reason (4) ✓ equation of AB ✓ coordinates of E ✓ gradient of EF ✓ gradient EF = gradient BG (4)
3.4	Midpoint of AC = (5;½) x_D + (6) = 5 and x_D + (-5) = ½ 2 2 ∴ D(16 ; 6) OR by translation: D(16 ; 6) OR m_BC = -5 -(-4) = 1 and m_AB = 5 -(-5) = 5 -6-8 14 2-(-6) 4 AD: y - 5 = 1 (x-2) → y = 5 x-14 4 4 5 x - 14 = 1 x + 34 4 14 7 ∴ x = 16 y = 6	✓✓(5;½) ✓ x value ✓ y value (4) ✓ method finding x ✓ method finding y ✓ x value ✓ y value (4) ✓✓ equating ✓ x value ✓ y value (4) [17]

QUESTION 4

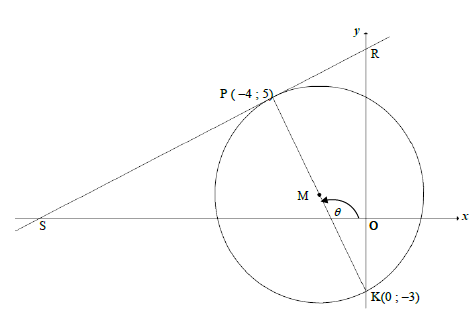
4.1.1	m_PK = 5 - (-3) -4 - 0 =-2 PK ⊥ SR [radius ⊥ tangent] ∴ m_PK x m_RS = -1 ∴ m_RS = ½	✓ substitution P & K into gradient formula ✓ gradient of PK ✓ PK ⊥ SR OR r ⊥ tangent ✓ answer (4)
4.1.2	y = ½x + c 5 = ½(-4) + c OR (y-5) = ½(x-(-4)) c = 7 (y - 5) = ½x + 2 y = ½x+7 y = ½x + 7	✓ substitution of m and P ✓ equation (2)
4.1.3	M(–2 ; 1) ∴ r ² = (x₂ - x₁)² + ( y₂ - y₁)² r ² = (-2 + 4)² + (1 - 5)² ∴ r ² = 20 ∴(x + 2)² + ( y - 1)² = 20 or √( 20)² OR (x + 2) ² + ( y - 1) ² = r ² (-4 + 2) ² + (5 - 1) ² = r ² ∴ r ² = 20 ∴ (x + 2)² + ( y - 1)² = 20 or √( 20)² OR	✓x value of M ✓y value of M ✓r ² = 20 ✓equation (4) ✓✓M (– 2 ; 1) ✓r ² = 20 ✓equation (4) ✓✓M (– 2 ; 1) ✓r ² = 20 ✓equation (4)
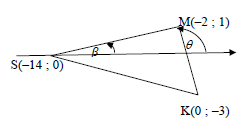
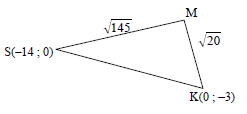
4.1.4	tanθ = m_PK = -2 ∴ q = 180° – 63,43° = 116,57° PKR = 116,57° - 90° [ext ∠ of ΔMOK] = 26,57° OR	✓tanθ = -2 ✓size of q ✓answer (3) ✓lengths of PK, PR & RK ✓correct values into cos rule ✓answer (3) ✓lengths of sides ✓ratio ✓answer (3) ✓lengths of sides ✓ratio ✓answer (3)
4.1.5	RS \|\| tangent at K(0 ; – 3 ) ∴ m_PS = m_tang =½ ∴ y = ½ x - 3 OR m_PK = 1- 5 = -2 - 2 + 4 m_PK x m_tang= -1 [radius ⊥ tangent] ∴ m_{tan g} = ½ ∴ y = ½ x - 3	✓gradient ✓equation (2) ✓gradient ✓equation (2)
4.2	t ∈ (-3 ; 7) OR - 3 < t < 7	✓– 3 (A) ✓7 (CA from 4.1.2) ✓correct inequality (3) ✓– 3 (A) ✓7 (CA from 4.1.2) ✓correct inequality (3)
4.3	RS: y = ½ x + 7 ∴S(–14 ; 0) SP = √(-14 - (-4))² + (0 - 5)² = √100 + 25 =√125 Area DSMK = ½ . MK . SP = ½(20)(√125) = 25 square units OR Let β = inclination of SM RS: y = ½ x + 7 ∴ S(–14 ; 0) SM = √(-14 - (-2))² + (0 -1)² = √145 tan β = 1 - 0 = 1 ∴ β = 4,76° - 2 - (-14) 12 ∴ SMK = 116,57° – 4,76° [ext Ð of D] = 111,81° Area ΔSMK = ½(SM)(MK).sinSMK = ½(√145)(√20).sin111,81° = 24,9985 = 25 square units OR RS: y = ½ x + 7 ∴ S(–14 ; 0) SK = √(-14 - 0)² + (0 + 3⁾² = √205 cosSMK = (√145)² + (√20)² - (√205)² = - 2√29 2( 145)( 20) 29 SMK = 111,80° Area ΔSMK = ½(SM)(MK).sinSMK =½(√145)(√20).sin111,81° = 24,9985 = 25 square units OR Produce KS to T RS: y = ½ x + 7 ∴S(–14 ; 0) SK = √(-14 - 0)² + (0 + 3)² = √205 SM = √(-14 - (-2))² + (0 -1)² = √145 m_SK = - 3 ⇒ TSˆO = 167,91° 14 m_SM = 1 ⇒MSO = 4,76° 12 MSK = 180° - 167,91° + 4,76° = 16,85° Area ΔSMK = ½(SM)(SK).sinMSˆK = ½(√145)(√205).sin16,85° = 24,9985 = 25 square units	✓coordinates of S ✓length of SP ✓correct base & height into Area rule ✓correct substitution ✓answer (5) ✓coordinates of S ✓length of SM ✓size of SMK ✓correct substitution into area rule ✓answer (5) ✓coordinates of S ✓length of SK ✓size of SMK ✓correct substitution into area rule ✓answer (5) ✓coordinates of S ✓length of SK & SM ✓size of MSK ✓correct substitution into area rule ✓answer (5)

QUESTION 5

5.1	sin(A - 360°).cos(90° + A) cos(90° - A).tan(-A) = sinA(-sinA) sinA(-tanA)	✓sin A ✓sin A ✓sin A ✓–tan A ✓tan A = sinA cosA ✓answer (6)
5.2.1	t ² = (√34) ² - (3) ²∴ t = – 5	✓substitution ✓answer (2)
5.2.2	tan b = - 5 3	✓correct ratio(1)
5.2.3	cos²b = 2 cos² β - 1	✓compound formula ✓substitution ✓simplification ✓answer (4) ✓compound formula ✓substitution ✓simplification ✓answer (4) ✓compound formula ✓substitution ✓simplification ✓answer (4)
5.3.1	LHS = sin(A + B) – sin(A – B) = sin A.cos B + cos A.sin B – (sin A. cos B – cos A. sin B) = sin A.cos B + cos A.sin B – sin A. cos B + cos A. sin B = 2cos A.sin B = RHS	✓compound formula ✓compound formula (2)
5.3.2	sin 77° - sin 43° = sin(60° + 17°) - sin(60° - 17°) = 2cos 60°.sin 17° = 2 x ½ sin17° = sin17° OR sin 77° - sin 43° = sin(60° + 17°) - sin(60° - 17°) = (sin 60° cos17° + cos 60° sin17°) - (sin 60° cos17° - cos 60° sin17°) = √3 cos17° + ½ sin17° -√ 3 cos17° + ½sin17° 2 2 = sin17°	✓60° + 17° ✓60° – 17° ✓simplify ✓½ (4) ✓60° + 17° ✓60° – 17° ✓simplify ✓½ (4) [19]

QUESTION 6

6.1		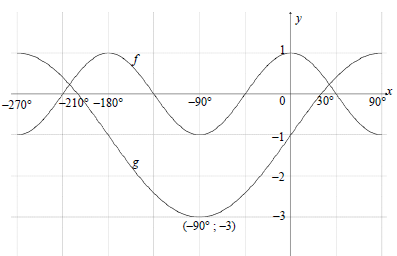✓(–90° ; –3) ✓(0 ; –1) ✓x – intercepts: –210° & 30° ✓shape (4)
6.2	cos 2x = 2 sin x - 1 1 - 2 sin²x = 2 sin x - 1 2sin ²x + 2 sin x - 2 = 0 sin ²x + sin x - 1 = 0	✓cos 2x = 1- 2 sin ²x ✓standard form ✓using quadratic formula ✓substitution into quadratic formula (4)
6.3	sin x = - 1 + √5 = 0,618... 2 Reference Ð = 38,17° ∴ x = 38,17° + k.360° or x = 141,83° + k.360° ; k∈ Z \ x = 38,17° or - 218,17° y = 0,24 Points of intersection (38,17° ; 0,24) and (-218,17° ; 0,24)	✓38,17° ✓141,83° ✓–218,17° ✓0,24 (4) [12]

QUESTION 7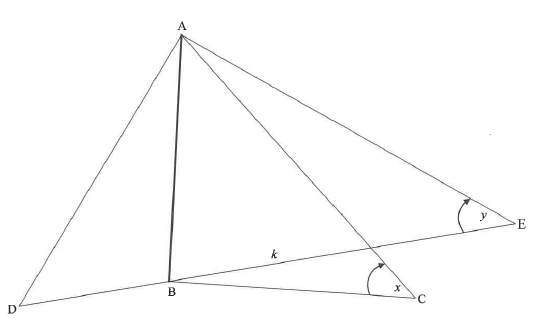

7.1

ABˆ C = 90°

✓answer (1)

7.2

In D ABE:
AB = tan y
BE

AB = k tan y

In D ABC:

AB = sin x
AC

AC = AB
sin x

= k tan y
sin x

✓correct ratio
✓value AB
✓correct ratio
✓AC as subject and substitution
(4)

7.3

ADˆ C = ACˆ D = 180° - 2x = 90° - x
2
DC   =   AC
sin2x     sin(90° - x)
DC    = AC
2 sin x cos x   cos x
DC = AC(2sin x cos x)
cos x
= k tan y - 2 sin x cos x
sin x          cos x
= 2k tan y

DC² = AD² + AC² - 2AD.ACcos 2x
= AC² + AC² - 2AC² cos 2x
= 2AC² (1- cos 2x)
= 2AC² (1- 1+ sin²x)
= 4AC² sin²x
DC = 2AC.sin x

✓90° - x
✓subst into sine rule
✓2 sin x cos x
✓ ü cos x
✓ substitution
(5)

✓substitution into cos rule
✓factorisation
✓1- 2 sin ²x
✓DC ito AC and sin x
✓substitution
(5)

✓correct cos rule
✓substitution
✓1- 2 sin ²x
✓squaring and multiplication
✓√4k ² tan²y
(5)

[10]

QUESTION 8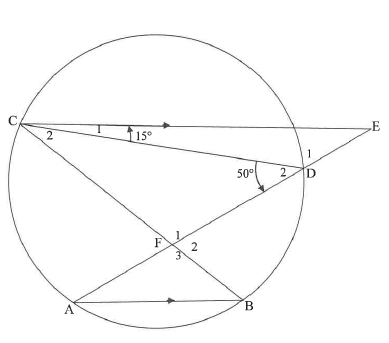

8.1.1

E = 50°- 15° = 35° [ext ∠ of D]
A = 35° [alt ∠s ; CE || AB]
OR
E = 180° - (130° + 15°) = 35° [str line; ∠s of D]
Aˆ = 35° [alt ∠se; CE || AB]

OR
B = 50° [∠s in same segment]
C₂ + 15° = 50° [alt ∠s ; CE || AB]
∴ C₂ = 35°
A = 35° [∠s in same segment]

✓S
✓S ✓R (3)

✓S ✓ R (3)
✓S

✓S

✓S ✓ R (3)

8.1.2

C₂ = 35° [Ðs in same segment]

✓S ✓R (2)

8.2

C₂ = E [from 8.1.1 and 8.1.2]
∴ CF is a tangent to the circle [converse tan chord theorem]

✓S
✓ R (2)
[7]

QUESTION 9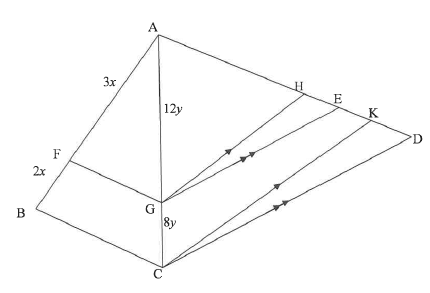

9.1.1

AF = 3x = 3 & AG = 12y = 3
BF 2x 2 CG 8y 2

∴ AF = AG
BF CG

∴ FG || BC [conv prop th. OR line divides 2 sides of ∆ in prop]

✓ AF = AG
BF CG

✓ R

(2)

9.1.2

AG = AH [prop theorem; GH || CK OR
GC HK
line || to 1 side of D]
AG = AE [prop theorem; GE || CD]
GC ED

∴ AH = AE
HK ED

✓S ✓R

✓ S

(3)

9.2

AE = 3 and AH = 3
ED 2 HK 2

AE = 3 and 15 = 3
12 2 HK 2

∴ AE = 18 and HK = 10               AD = 30
∴ HE = AE – AH                           KD = AD – AH – HK
= 18 – 15                                     = 30 – 15 – 10
= 3                     OR = 5

∴ EK = HK – HE                           EK = ED – KD
= 10 – 3                                      = 12 – 5
= 7                                              = 7

✓use of ratios
✓ AE = 18
✓ HK = 10
✓ HE = 3 or KD = 5
✓ EK = 7
(5)

[10]

QUESTION 10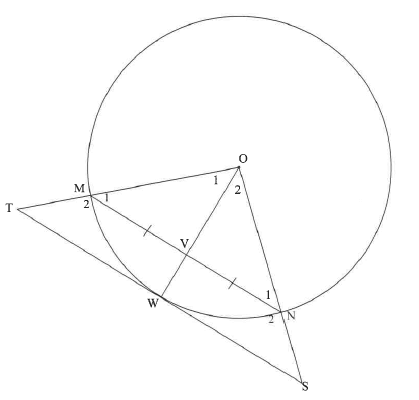

10.1	Line from centre to midpoint of chord	✓ R (1)
10.2.1	OWT = OWS = 90° [radius ^ tangent] ∴ MN \|\| TS [corresp ∠s = OR co-int Ðs 180° OR alternate ∠ s]	✓ R ✓ R (2)
10.2.2	M₁ = N₁ [∠s opp = sides] M₁ = T [corresp ∠s; MN \|\| TS] ∴ N₁ = T ∴TMNS is a cyclic quadrilateral [conv: extÐ cyclic quad] OR M₁ = N₁ [∠s opp = sides] N₁ = S [corresp ∠s; MN \|\| TS] ∴ S = M₁∴ TMNS is a cyclic quadrilateral [conv: extÐ cyclic quad]	✓ S ✓ S ✓ S ✓ R (4) ✓ S ✓ S ✓ S ✓ R (4)
10.2.3	In ΔOVN and ΔOWS O₂ = O₂ [common] ΔOVN = ΔOWS = 90° [from 10.1] ΔONV = ΔOSW [sum ∠s Δ] ∴ΔOVN \|\|\| DOWS [∠, ∠, ∠] ∴ VN = ON WS OS But VN = ½ MN [given] ½MN= ON WS OS ∴ OS.MN = 2ON. WS OR In ΔOVM and ΔOWS ΔOVM = ΔOWS = 90° [from 10.1] ΔOMV = ΔOSW [sum ∠s Δ] ∴ΔOVM \|\|\| ΔOWS [∠,∠,∠] ∴ OM = VM OS WS But VN = ½MN [given] ½MN= OM WS OS ∴ OS.MN = 2ON. WS [VM = VN] OR If any other 2 Ds are used, first need to prove that TW = WS by proving ΔOWT ≡ ΔOWS In ΔOVM and ΔOWT O₁ = O₁ [common] OVM = OWT = 90° [from 10.1] OMV = OTW [sum ∠s ∠] ∴ΔOVM \|\|\| ΔOWT [∠,∠,∠] ∴ VM = OM WT OT But VN = VM = ½MN [given] and WT = WS and OT = OS [ΔOWT ≡ ΔOWS] ½MN= ON WS OS ∴ OS.MN = 2ON. WS	✓S; S; S OR S; S; R ✓ΔOVN \|\|\| ΔOWS ✓VN = ON WS OS ✓ VN = ½MN ✓ substitution (5) ✓S; S; S OR S; S; R ✓ΔOVM \|\|\| ΔOWS ✓OM = VM WS OS ✓ VN = ½MN ✓ substitution (5) ✓✓similarity ✓✓congruency ✓VN = VM =½ MN (5) [12]

QUESTION 11

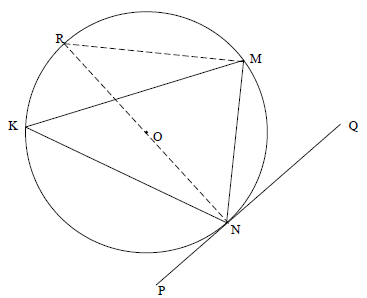
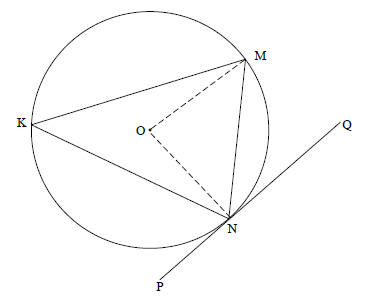
11.1

Construction: Draw diameter NR and draw RM
ONM + MNQ = 90°           [ radius ^ tangent
NMR = 90°                        [∠ in semi circle]
∴ MRN =180° - (90° + 90° - MNˆ Q)      [sum ∠s Δ]
= MNQ

but MRN = MKN [Δs same segment]
∴ MNQ = K

✓construction
✓S /R
✓S/ R
✓S
✓S / R
(5)

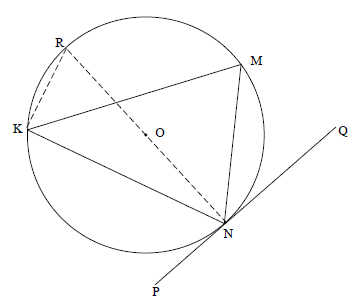
11.1

Construction: Draw diameter NR and draw RK
MNQ + RNM = 90° [radius ^ tangent]
NKR = 90° [∠ in semicircle]
∴ MKN = 90° - RKM
= 90° – RNM [∠s same segment]
∴ MNQ = K

✓construction
✓S /R
✓S/ R
✓S
✓S / R
(5)

11.1

Construction: Draw radii ON and OM
MON = 2K [ at centre = 2∠ at circumf]
ONM + OMN = 180° - 2Kˆ [ ∠s of D]
ONM = OMN = 180° - 2K = 90° - Kˆ [∠s opp = sides]
2
ONQ = 90° [radius^tangent]
∴ MNQ = K

✓construction
✓S /R
✓S
✓S/ R
✓S / R
(5)

11.2

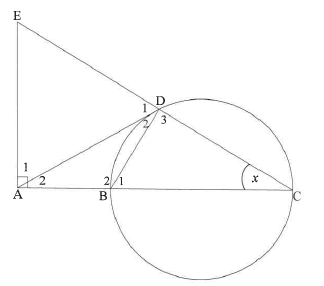
11.2.1(a)	Angle in a semi circle	✓R (1)
11.2.1(b)	Exterior ∠ of quad = opp interior OR Opp ∠s of quad supplementary	✓R (1)
11.2.1(c)	tangent chord theorem	✓R (1)
11.2.2(a)	In ΔAEC Eˆ = 180° - (90° + x) [sum ∠s Δ] = 90° x D1 = 180° - (90° + x) [∠s on a straight line] = E = 90° - x ∴ AD = AE [sides opp = ∠s]	✓S ✓S ✓R (3)
11.2.2(b)	In ΔADB and ΔACD A₂ = A₂ [common] D₂ = C [proven] B₂= D₂ + D₃ [sum ∠^e Δ] ∴ΔADB \|\|\| ΔACD OR In ΔADB and ΔACD A₂ = A₂ [common] D₂ = C [proven] ∴ΔADB \|\|\| ΔACD [∠,∠,∠]	✓S ✓S ✓S (3) ✓S ✓S ✓R (3)
11.2.3(a)	AD = AB [\|\|\| ∠s] AC AD AD² = AC . AB = 3r × r = 3r²	✓ratio ✓substitution (2)
11.2.3(b)	AD = AE = √3r [from 11.2.2(a) &11.2.3(a)] AB = r and BC = 2r ∴AC = 3r In ΔACE: tan Eˆ = AC AE = 3r = √3 √3r ∴ E = 60° ∴ D1 = 60° [from 11.2.2(a)] ∴ Aˆ 1 = 60° [∠s of Δ = 180°] ∴ Δ ADE is equilateral OR AD = DB [\|\|\| Δs] AC CD √3r = DB 3r CD tan x = 1 √3 ∴ In ΔBDC: x = 30° ∴ E = 60° ∴ D1 = 60° [from 11.2.2(a)] ∴ A1 = 60° [∠s of Δ = 180°] ∴ ΔADE is equilateral OR AD = DB [\|\|\| Ds] AC CD √3r = DB ∴ BD = CD 3r CD √3 DC² = BC² - DB²=4r² - CD² 3 3DC² = 12r² - CD²4CD² = 12r²DC = √3r EC² = EA² + AC²= 3r² + 9r²EC = 2√3r ∴ ED = EC – DC = √3r ∴ ED = EA = AD ∴ DADE is equilateral	✓AC ito r ✓trig ratio ✓simplification ✓all 3 ∠s = 60° (4) ✓√3r = DB 3r CD ✓ 1 = tan x √3 ✓x = 30° ✓all 3 ∠s = 60° (4) ✓BD = CD √3 ✓DC = √3r ✓EC = 2√3r ✓ED = EA = AD (4) [20]

TOTAL:150

Last modified on Friday, 10 September 2021 09:48

Published in Grade 12 NSC Exam Past Papers and Memos November 2017

GRADE 12 MATHEMATICS PAPER 2 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2017

Related items