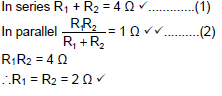PHYSICAL SCIENCES PAPER 1 GRADE 12 MEMORANDUM - NSC PAST PAPERS AND MEMOS NOVEMBER 2017
Share via Whatsapp Join our WhatsApp Group Join our Telegram GroupPHYSICAL SCIENCES: PHYSICS (PAPER 1)
GRADE 12
NOVEMBER 2017
MEMORANDUM
NATIONAL SENIOR CERTIFICATE
QUESTION 1
1.1 B ✓✓ (2)
1.2 D ✓✓ (2)
1.3 A ✓✓(2)
1.4 C✓✓ (2)
1.5 B✓✓ (2)
1.6 A✓✓ (2)
1.7 D✓✓ (2)
1.8 B✓✓ (2)
1.9 C✓✓ (2)
1.10 D✓✓ (2)
[20]
QUESTION 2
2.1.1 An object continues in its state of rest or uniform motion (moving with constant velocity) unless it is acted upon by an unbalanced (resultant/net) force.✓✓
OR
A body will remain in its state of rest or motion at constant velocity unless a resultant/net force acts on it.✓✓
OR
A body will remain in its state of rest or of uniform motion in a straight line at constant velocity/speed unless a non-zero resultant/net force acts on it.✓✓ (2)
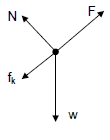
2.1.3
| Accepted Labels | |
| w | Fg / Fw/weight/mg /78,4 N/gravitational force |
| F | Fapp/FA / applied force (Accept T / tension) |
| fk | (kinetic) Friction/Ff/f/(kineties) wrywing/Fw |
| N | FN/Normal (force)/Normaal(krag)/ 67,9 N |
(4)
2.1.3
| Fnet = ma ✓ Fnet = 0 F+(-fk) + (-Fgll) = ma F- (fk + Fgll ) = ma F - 20,37✓ - (8)(9,8)sin30o✓ = 0 F = 59,57 N ✓ (5) |
2.1.4
| OPTION 1 Fnet = ma (Fg|| - fk) = ma (8)(9,8)sin30o - 20,37✓ = 8a ✓ ∴magnitude: a = 2,35 m·s-2✓ | OPTION 2 Fnet = ma (Fg|| - fk) = ma 20,37 + [-(8)(9,8)sin30o]✓ = 8a ✓ ∴a = -2,35 m·s-2 ∴ magnitude: a = 2,35 m·s-2✓ |
(4)
2.2.1 Each body in the universe attracts every other body with a force that is directly proportional to the product of their masses ✓ and inversely proportional to the square of the distance between their centres. ✓
OR
Every particle in the universe attracts every other particle with a force along a line joining them. The force is directly proportional to the product of the masses ✓ of the particles and inversely proportional to the square of the distance between them. ✓ (2)
2.2.2
| OPTION 1 g = GM r2 6 = (6,67 x 10-11)M (700 x 103)2 M = 4,41 x 1022 kg ✓ | OPTION 2 F = Gm1m2 r2 mg = GmM r2 (200)(6) = (6,67 x 10-11)(200)M (700 x 10-3)2 M = 4,41 x 1022 kg ✓ |
(4)
[21]
QUESTION 3
3.1
| OPTION 1 Upwards positive vf = vi + aΔt✓ 0 = (12) + (-9,8)(Δt) ✓ Δt = 1,22 s✓ | Downwards positive vf = vi + aΔt✓ 0 = (-12) + (9,8)(Δt) ✓ Δt = 1,22 s✓ |
| OPTION 2 Upwards positive vf2 = vi2 + 2aΔy 0 = 122 + 2(-9,8)Δy✓ Δy = 7,35 Δy = viΔt + ½ aΔt2✓ 7,35 =12Δt + ½ (-9,8)Δt2 Δt = 1,22 s✓ | Downwards positive vf2 = vi2 + 2aΔy 0 = (-12)2 + 2(9,8)Δy✓ Δy = -7,35 Δy = viΔt + ½ aΔt2✓ -7,35 = -12Δt + ½ (9,8) Δt2 Δt = 1,22 s✓ |
OPTION 3
| Downwards positive vf2 = vi2 + 2aΔy 0 = 122 + 2(-9,8)Δy✓ Δy = -7,35 m 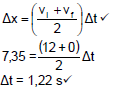 |
| OPTION 4 (E mech)A= (E mech)top (½ mv2 + mgh)A = (½ mv2 + mgh)top ½m(12)2 + 0 = 0 + m(9,8)(h) ✓ ∴h = Δy = 7,35 m | 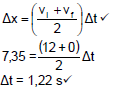 |
| OR Wnet = ΔEk FnetΔycosθ = ½ m(vf2 – vi2) m(9,8)Δycos 180o = ½ m(02 – (12)2)✓ Δy = 7,35 m | |
| OR ΔEp + ΔEk = 0 mg(hf – hi) + ½ m(vf2 – vi2) = 0 m(9,8)(h – 0) + ½(m)(0 - 122) = 0✓ ∴h = Δy = 7,35 m | |
| OPTION 5 Upwards positive FnetΔt = m(vf - vi) ✓ mgΔt = m(vf - vi) (-9,8)Δt = (0 – 12) ✓ Δt = 1,2245 s ✓ | Downwards positive FnetΔt = m(vf - vi) ✓ mgΔt = m(vf - vi) (9,8)Δt = (0 – (-12)) ✓ Δt = 1,2245 s ✓ |
| OPTION 6 Upwards positive Δy = viΔt + ½ aΔt2 ✓ 0 = 12Δt + ½ (-9,8)Δt2 Δt = 2,4490 s Δt = ½ (2,4490)✓ = 1,2245 s ✓ | Downwards positive Δy = viΔt + ½ aΔt2 ✓ 0 = -12Δt + ½ (9,8)Δt2 Δt = 2,4490 s Δt = ½ (2,4490) ✓ = 1,2245 s ✓ |
(3)
3.2
| OPTION 1 Upwards positive vf = vi + aΔt✓ -3v = -v✓ + (-9,8)(1,22) ✓ v = 5,98 m∙s-1✓(5,978 – 6,03 m∙s-1) | Downwards positive vf = vi + aΔt✓ 3v = v✓ + (9,8)(1,22) ✓ v = 5,98 m∙s-1✓(5,978 – 6,03 m∙s-1) |
| OPTION 2 Upwards positive FnetΔt = m(vf - vi) ✓ mgΔt = m(vf – vi) (-9,8)(1,2245)✓ = -3v – (-v)✓ v = 6,00 m∙s-1 ✓ | Downwards positive FnetΔt = m(vf - vi) ✓ mgΔt = m(vf – vi) (9,8)(1,2245)✓ = 3v - v✓ v = 6,00 m∙s-1 ✓ |
(4)
3.3
| OPTION 1 Upwards positive Δy = viΔt + ½aΔt2✓ = (-5,98)(2,44) + ½(-9,8)(2,44)2✓ = - 43,764 ∴h = 43,76 m✓ (43,764 – 44,08 m) | Downwards positive Δy = viΔt + ½aΔt2✓ = (5,98)(2,44) + ½(9,8)(2,44)2 ✓ = 43,764 ∴h = 43,76 m✓(43,764 – 44,08) |
| OPTION 2 Upwards positive vf = vi + aΔt vf = - 5,98 + (-9,8)(2,44) vf = - 29,892 m·s-1 vf2 = v2 + 2aΔy (-29,892)2 = (- 5,98)2 + 2(-9,8)Δy✓ Δy = - 43, 763 m ∴h = 43,76 m(43,764 – 44,08) | Downwards positive vf = vi + aΔt vf = 5,98 + 9,8(2,44) = 29,892 m·s-1 vf2 = v2 + 2aΔy (-29,892)2 = (- 5,98)2 + 2(-9,8)Δy✓ Δy = - 43, 763 m ∴h = 43,76 m✓(43,764 – 44,08) |
| OPTION 3 Upwards positive vf = vi + aΔt vf = - 5,98 + (-9,8)(2,44) vf = - 29,892 m·s-1 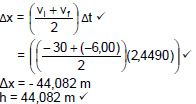 | Downwards positive
|
| OPTION 4 Upwards positive For A vf = vi + aΔt -12 = 12 + (-9,8)Δt Δt = 2,45 s For B Δx = viΔt + ½ aΔt2 ✓ = (-5,98)(2,45) + ½ (-9,8)(2,45)2 ✓ = - 44,06 m h = 44,06 m ✓ | Downwards positive For A vf = vi + aΔt 12 = -12 + (9,8)Δt Δt = 2,45 s For B Δx = viΔt + ½ aΔt2 ✓ = (5,98)(2,45) + ½ (9,8)(2,45)2 ✓ = 44,06 m h = 44,06 m ✓ (3) |
| OPTION 5 Upwards positive Δy = viΔt + ½aΔt2 ✓ ΔyA = 12Δt + ½ aΔt2 ΔyB = -6Δt + ½ aΔt2 ΔyA – ΔyB = 12Δt – (-6Δt) 0 – ΔyB = 18Δt ✓ = 18(2,44) = 43,92 m h = 43,92 m ✓ | Downwards positive Δy = viΔt + ½aΔt2 ✓ ΔyA = -12Δt + ½ aΔt2 ΔyB = 6Δt + ½ aΔt2 ΔyA – ΔyB = 12Δt – (-6Δt) 0 – ΔyB = -18Δt ✓ = -18(2,44) = 43,92 m h = 43,92 m ✓ (3) |
| OPTION 6 Upwards positive Wnet = ΔEk ✓ mgΔycosθ = ½ m(vf2 – vi2) (-9,8)hcos0o = ½ (-20)2 – ½ (-6)2✓ h = 44,082 m ✓ | Downwards positive Wnet = ΔEk ✓ mgΔycosθ = ½ m(vf2 – vi2) (9,8)hcos0o = ½ (20)2 – ½ (6)2 ✓ h = 44,082 m ✓ |
| OPTION 7 (Ep + Ek)top = (Ep + Ek)bottom mghi + ½ mvi2 = mghf + ½ mvf2 (9,8)h + ½ (6)2 = (9,8)(0) + ½ (30)2 ✓ h = 44,082 m ✓ (3) | |
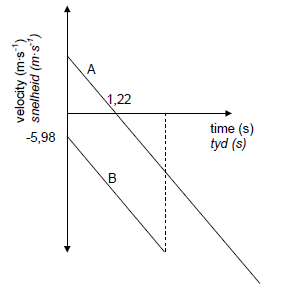
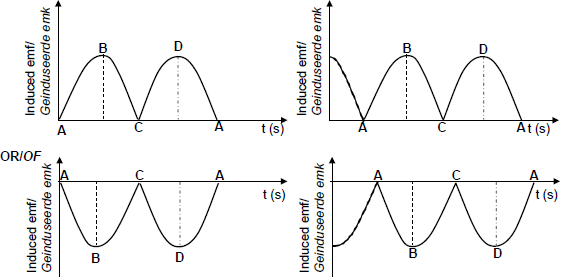
3.4 UPWARDS AS POSITIVE
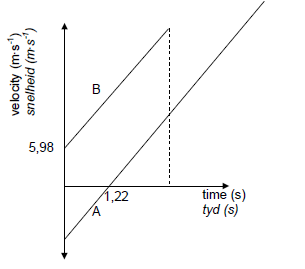
DOWNWARDS AS POSITIVE
| Criteria for graph | Marks |
| Time 1,22 s shown correctly | ✓ |
| Initial velocity for stone B at time t = 0 correctly shown with correct signs | ✓ |
| Two sloping parallel lines with A crossing the time axis | ✓ |
| Straight line graph for A parallel to graph B, extending beyond the time when B hits the ground | ✓ |
(4)
[14]
QUESTION 4
4.1 The total linear momentum in an isolated/closed system is constant.✓✓
OR
In an isolated/closed system, total linear momentum before collision is equal to total linear momentum after collision. ✓✓ (2)
4.2 Σpi = Σpf ✓
mBvBi + mbvbi = mBvBf + mbvbf
Δpbullet = -Δpblock
(0,015)(400)✓ + 0 = (0,015)vBf + 2(0,7)✓
VBf = 306,67 (306,666)m∙s-1✓ (4)
4.3
OPTION 1 Wnet = ΔEk | |
| Fnet = ma -700 = (0,015)a OR Fmet = ma 700 = (0,015)a a = - 46 666,67 or 46 665 m·s-2 | Δx = viΔt + ½ aΔt2 = (400)(0,002) + ½(-46 666,67)(0,002)2✓ = 0,71 m (0,70667) m✓ |
| OR vf2 = vi2 + 2aΔx (306, 67)2 ✓= (400)2 + 2(-46 666,67)Δx✓ Δx = 0,71 m (0,70667 m) ✓ | |
| OPTION 2 vf = vi + aΔt✓ 306,666 = 400 + a (0,002) ✓ a = -46 667 m·s-2 vf 2 = vi 2 + 2aΔx (306,666)2 ✓= 4002 + 2(-4667) Δx✓ Δx = 0,71 m (0,706 m) ✓ | |
OPTION 3 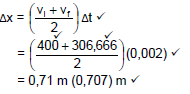 | |
| OPTION 4 Wnet = ΔK/ΔEk ✓ FnetΔxcos θ = maΔxcosθ = ΔK/ΔEk vf = vi + aΔt 306,666 = 400 + a (0,002) ✓ a = -46 667 m·s-2 | |
| Wnet = ΔK/ΔEk FnetΔxcos θ = maΔxcosθ = ΔK/ΔEk (0,015)(46 667)Δxcos180o✓ = ½(0,015)(306,6662 – 4002)✓ Δx = 0,71 m (0,707) ✓ | |
| OR Wnc = ΔEp + ΔEk (0,015)(46 667)Δxcos180o✓ = ½(0,015)(306,6662 – 4002)✓ Δx = 0,71 m (0,707) ✓ | |
(5)
[11]
QUESTION 5
5.1 The net/total work done (on an object) is equal to the change in the object's kinetic energy.✓✓
OR
The work done on an object by a resultant/net force is equal to the change in the object's kinetic energy.✓✓(2)
5.2
| Accepted labels | |
| w | Fg / Fw / weight / mg/ 58,8N / gravitational force / Fearth on block |
| T | FT/ Tension/ spannin |
5.3
| Ww = wΔxcosθ✓ = mgΔxcosθ = (6)(9,8)(1,6)cos0o✓ ∴W = 94,08 J ✓ | Ww = - ΔEP ✓ = - mg(hf – hi) = - (6)(9,8)(0 – 1,6) ✓ = 94,08 J✓ |
(3)
5.4
| OPTION 1 Wnet = ΔEK /ΔK✓ = ½m(vf2 – vi2) Wnet = FnetΔxcosθ Wnet = Wf + Wg + WN = μkNΔxcosθ + Wg + WN Wnet = (0,4)(4)(9,8)(1,6)cos180o ✓ + 94,08 + 0 = 68,992 J Wnet = ½m(vf2 – vi2) 68,992✓= ½(4)(vf2 – 0) + ½(6)(vf2 – 0)✓ vf = 3,71 m∙s-1✓ | |
| OPTION 2 Wnc = ΔEp + ΔEk ✓ fΔxcosθ = (m1ghf – m1ghi) + (½m1vf2 - ½m1vi2) + (½m2vf2 - ½m2vi2) (0,4)(4)(9,8) (1,6) cos 180o ✓= [0 - (6)(9,8)(1,6)]✓+ (½(6)vf2 + ½(4)vf2 - 0)✓ 68,992 = 5vf2 vf = 3,71 m∙s-1✓ | |
| OPTION 3 fk = μkN = (0,4)(4)(9,8) = 15,68 N T – fk = ma w – T = ma T – 15,68 = 4a … .(i) (6)(9,8) – T = 6a ……..(ii) ∴a = 4,312 m·s-2 ∴T = 32,928 N | Fnet = ma = (6)(4,312) = 25,872 Wnet = FnetΔxcosθ = (25,872)(1,6)cos0o✓ = 41,3952 J Wnet = ΔEk 41,3952 = ½ m(vf2 – vi2 41,3952 = ½ (6)(vf2 – 0)✓ vf = 3,7146 m∙s-1✓ Above calculations can be done with 4 kg or 10 kg |
| 4 kg block Wnet = ΔEK /ΔK✓ Wf + WT = ½m(vf2 – vi2) fΔxcos180o + TΔxcos0o = ½(4)(vf2 – 0) (15,68)(1,6)(-1)✓ + (32,928)(1,6)(1)✓ = 2vf2 vf = 3,72 m·s-1✓ | 6 kg block Wnet = ΔEK /Δ K✓ Ww + WT = ½m(vf2 – vi2) mgΔxcos0o + TΔxcos180o = ½(6)(vf2 – 0) (6)(9,8)(1,6)(1)✓+ (32,928)(1,6)(-1)✓= 3vf2 vf = 3,72 m·s-1✓ |
| OPTION 4 Wnet = ΔEK /ΔK ✓ For the 4 kg mass T(1,6)cos0o + [(0,4)(9,8)(4)](1,6)cos180o✓= ½(4)v2 – 0) For the 6 kg mass (6)(9,8)(1,6)]cos0o+ T(1,6)cos180o✓ = ½(6)(v2 – 0) Adding the two equations / Optel van twee vergelykings 68,992 = ½ (4)v2 + ½ (6)v2 ✓ 5v2 = 68,992 v = 3,71 m·s-1✓ | |
| OPTION 5 Wnet = ΔEk ✓ Fnet Δxcosθ = ½ m(vf2 –vi2) (Fg – f)Δxcosθ = ½m(vf2 –vi2) [(6)(9,8) – (0,4)(4)(9,8)]✓(1,6)cos0o ✓= ½(10)(vf2 - 0)✓ vf = 3,71m.s-1 ✓ | |
(5)
[12]
QUESTION 6
6.1 It is the (apparent) change in frequency (or pitch) of the sound (detected by a listener) ✓because the sound source and the listener have different velocities relative to the medium of sound propagation. ✓
OR
An (apparent) change in (observed/detected) frequency (pitch), (wavelength)✓ as a result of the relative motion between a source and an observer ✓ (listener). (2)
6.2.1 170 Hz✓ (1)
6.2.2 130 Hz✓ (1)
6.3
POSITIVE MARKING FROM QUESTIONS 6.2.1 and 6.2.2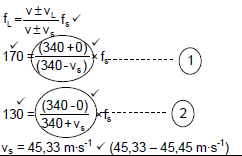 |
(6)
[10]
QUESTION 7
7.1 The magnitude of the electrostatic force exerted by one point charge on another point charge is directly proportional to the product of the (magnitudes of the) charges✓and inversely proportional to the square of the distance (r) between them. ✓
OR
The force of attraction or repulsion between two point charges is directly proportional to the product of the charges ✓ and inversely proportional to the square of the distance between them. ✓ (2)
7.2
| OPTION 1 F = k Q1Q2 r2 = (9x109((6x10-6)(8x10-6) (0,2)2 = 10,8 N✓ OPTION 2 E = kQ = (9x109((6x10-6)(8x10-6) = 1,8 x 104 N-C-1 r2 (0,2)2 F = Eq = (1,8 x 104)(6 x 10-6)✓ = 10,8 N✓ (4) |
7.3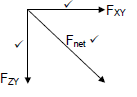
7.4
| OPTION 1 Fnet2 = FXY2 + FZY2 15,202 = 10,82 + Fzy2 FZY = 10,696 N FZY =k QZQY r2 10,696✓ = 9 x 109 x 8 x 10-6 x QZ (0,30)2 QZ = 1,34 x 10-5 C✓ |
| OPTION 2 cosθ = 10,8 15,2 θ = 44,72o sin 44,72 = FZY ✓ OR tan 44,72 = FZY 15,2 FXY FZY = 10,696 N FZY =k QZQY r2 10,696✓ = 9 x 109 x 8 x 10-6 x QZ (0,30)2 QZ = 1,34 x 10-5 C✓ 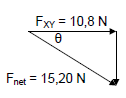 |
(4)
[13]
QUESTION 8
8.1 Electric field at a point is the force per unit positive charge placed at that point. ✓✓(2)
8.2 E = kQ✓
r2
Enet = (EA + EB)
= 9 x 109 (1,5 x 10-6) + 9 x 109 (2,0 x 10-6)
(0,4)2 (0,3)2
= 2,84 x 105 N∙C-1 ✓ (4)
8.3
| OPTION 1 FE = qE ✓ = (3,0 x 10-9)( 2,84 x 105) ✓ = 8,52 x 10-4 N ✓ |
| OPTION 2 F=k Q1Q2 r2 Fnet = (FA + FB) (3) |
[9]
QUESTION 9
9.1.1 The potential difference (voltage) across a conductor is directly proportional to the current in the conductor at constant temperature. ✓✓
OR
The current in a conductor is directly proportional to the potential difference (voltage) across the conductor if temperature is constant✓✓ (2)
9.1.2 (Equivalent) resistance✓ (1)
9.1.3 Gradient = ΔV
Δl
= 2-0 = 4 (Ω)✓
0,5-0
(2)
9.1.4 OPTION 1
OPTION 2
For graph X:
(4)
9.2.1 I = V
R
= 5
(RM + RN)
= 5
(6)
= 0,83 A✓ (3)
9.2.2
| OPTION 1 Ɛ = I(R + r) ✓ = 0,83[(6 +1,5) ✓+ 0,9✓] = 6,997 V = 7(,00) V✓ (6,972 – 7,00 V) | OPTION 2 Ɛ = (Vs + V// + Vr )✓ / Vext + Vint = [5 + (0,833 x 1,5) ✓+ (0,9 x 0,833)] ✓ = 6,999 V = 7(,00) V✓ (6,972 – 7,00 V) |
9.2.3 The resistance RN will be 3 Ω ✓
The voltage divides (proportionately) in a series circuit. Since the voltage across M is half the total voltage, it means the resistances of M and N are equal.✓(2)
[18]
QUESTION 10
10.1
10.1.1 Mechanical to electrical ✓ (1)
10.1.2
| Criteria for graph | Marks |
| Correct DC shape, starting from zero | ✓ |
| Positions ABCDA correctly indicated on the graph | ✓ |
(2)
10.2.1 20,5 Ω✓ (1)
10.2.2
| OPTION 1 Irms = Vrms = 25 R 20,5 = 1,22 (1,2195) A | ||
| Pave = Irms2R =(1,22)2(0,5) = 0,74 W Pave = Vrms2 R Pave = (25 )2 20,5 Pave = 30,49 W Actual energy delivered per second(power) = (30,49– 0,74) = 29,75 W✓ | Pave = Irms2 R✓ = (1,22)2(20) ✓ = 29,77 W✓ OR Vrms device = 20 × 25= 24,39 V 20,5 Pave = VrmsIrms ✓ = (24,39)(1,22) = 29,76 W ✓ | W = I2rms RΔt = (1,22)2 (0,5)(1) = 0,74 J Pave = Vrms2 R Pave = (25 )2 20,5 Pave = 30,49 W Actual energy delivered per second(power) = (30,49– 0,74) = 29,75 W✓ |
| OPTION 2 Vrms device = 20 × 25= 24,39 V 20,5 Pave = Vrms2 = (24,9) 2 = 29,76 W ✓ R 20 | ||
(5)
[9]
QUESTION 11
11.1.1 (Line) emission (spectrum) ✓ (1)
11.1.2 (Line) absorption (spectrum )(1)
11.2.1 Emission ✓(1)
11.2.2
| Energy released in the transition from E4 to E2 = E4 – E2 E4 – E2 = (2,044 x 10-18 – 1,635 x 10-18)✓ = 4,09 x 10-19J E = hf✓ 4,09 x 10-19 = (6,63 x 10-34)f✓ f = 6,17 x 1014 Hz✓ (4) |
11.2.3
| E = W0 + Ek(max) hf = hf0 + Ek(max) hf = hf0 + ½ mv2max E = W0 + ½ mv2max 4,09 x 10-19 ✓ = (6,63 x 10-34)(4,4 x 1014)✓ + Ek(max) Ek(max) = 1,17 x 10-19 J✓ OR Ek(max) = Elight – Wo = hflight – hfo = (6,63 x 10-34)( 6,17 x1014) ✓- (6,63 x 10-34)(4,4 x 1014)✓ = 1,17 x 10-19 J ✓ (4) |
11.2.4 No✓
The threshold frequency is greater than the frequency of the photon.✓
OR
The frequency of the photon is less than the threshold frequency✓
OR
Energy of the photon is less than the work function of the metal✓ (2)
[13]
TOTAL: 150